We introduce the unit step function and some of its applications.

The Unit Step Function

In the next section we'll consider initial value problems where , , and are constants and is piecewise continuous. In this section we'll develop procedures for using the table of Laplace transforms to find Laplace transforms of piecewise continuous functions, and to find the piecewise continuous inverses of Laplace transforms.

Use the table of Laplace transforms to find the Laplace transform of

PIC

Since the formula for changes at , we write To relate the first term to a Laplace transform, we add and subtract in (eq:8.4.2) to obtain To relate the last integral to a Laplace transform, we make the change of variable and rewrite the integral as

Since the symbol used for the variable of integration has no effect on the value of a definite integral, we can now replace by the more standard and write This and (eq:8.4.3) imply that Now we can use the table of Laplace transforms to find that

Laplace Transforms of Piecewise Continuous Functions

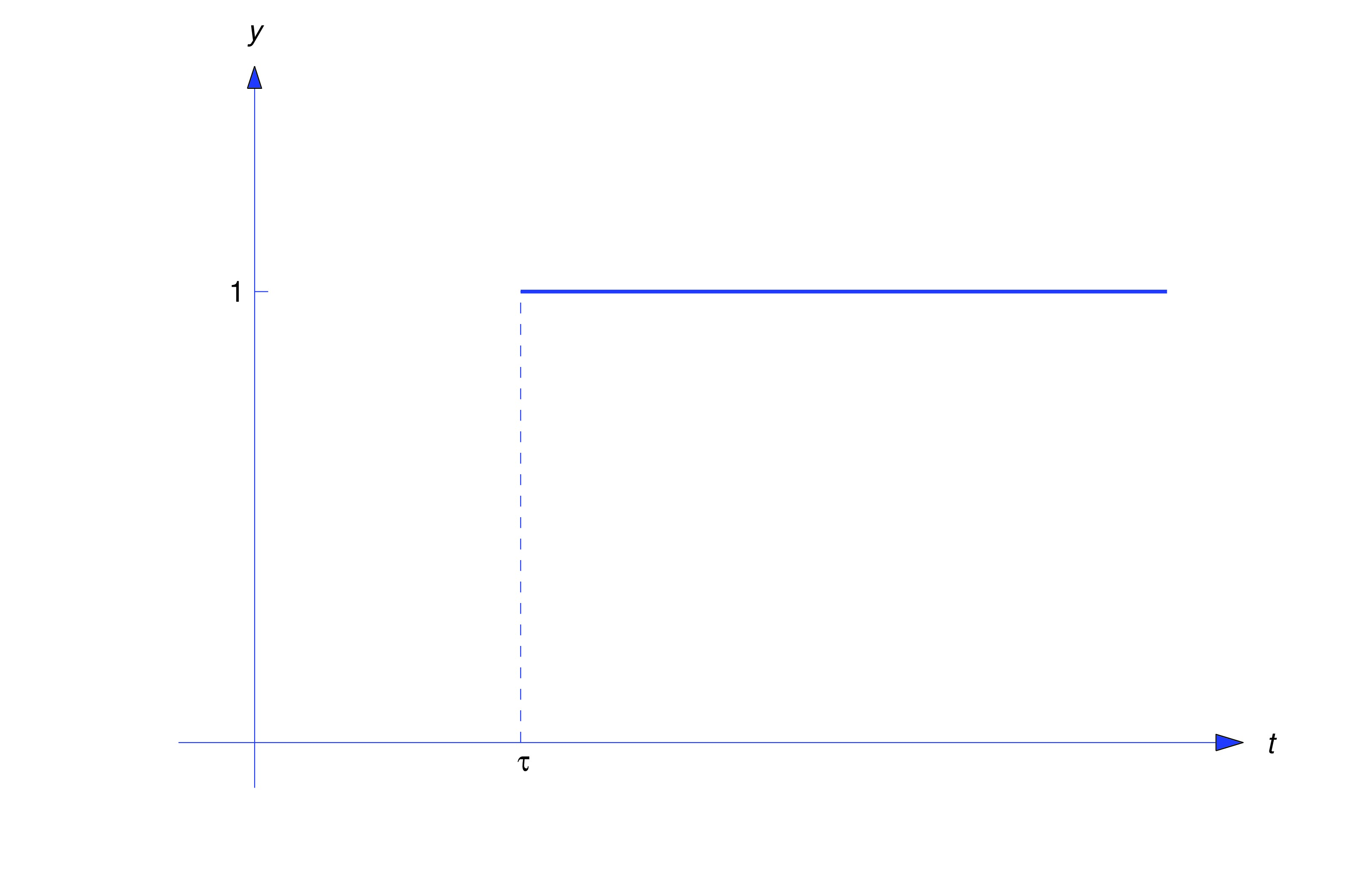
We'll now develop the method of Example example:8.4.1 into a systematic way to find the Laplace transform of a piecewise continuous function. It is convenient to introduce the unit step function, defined as

Thus, "steps" from the constant value to the constant value at . If we replace by in (eq:8.4.4), then that is, the step now occurs at (See figure below)

PIC

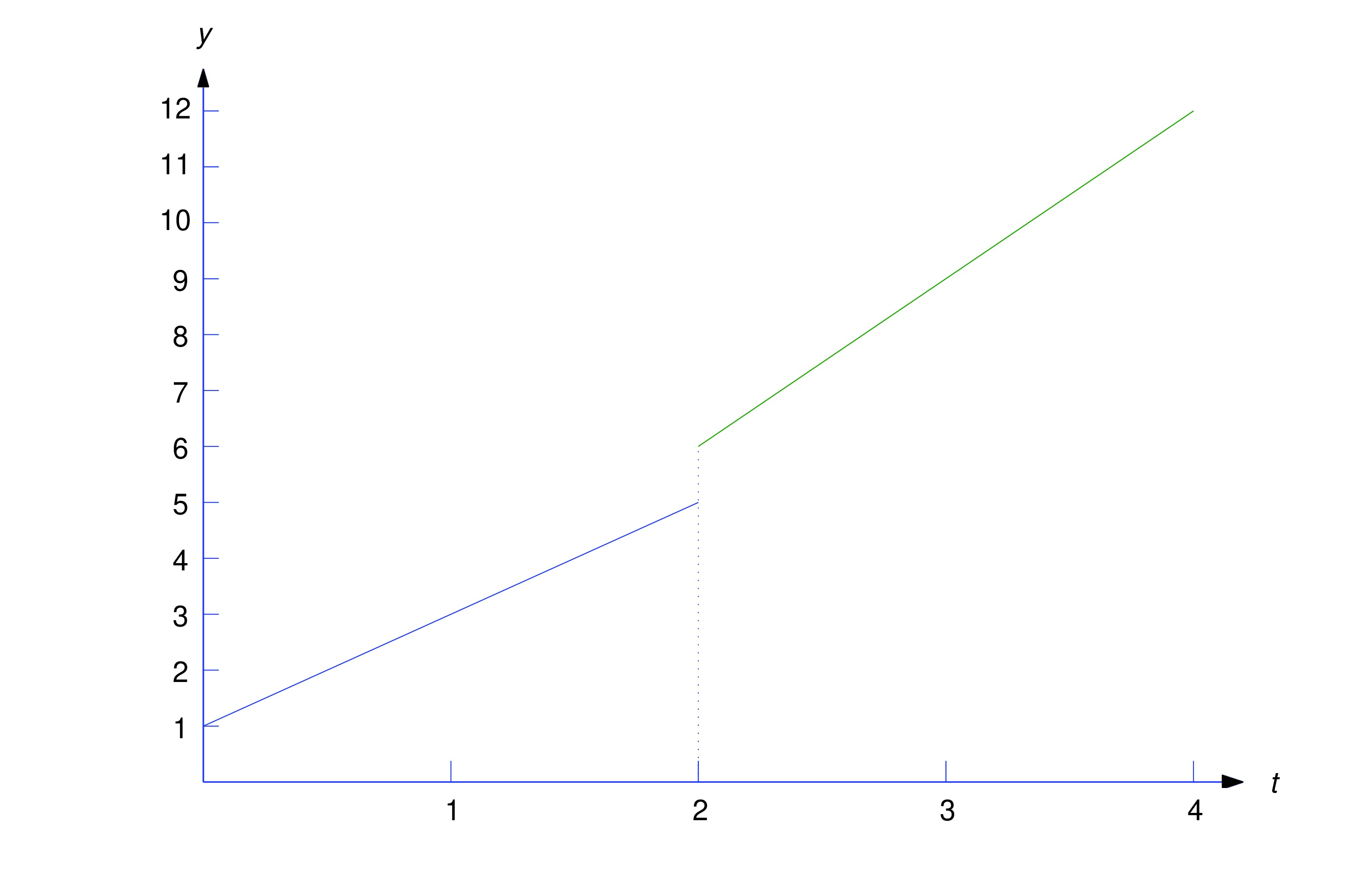
The step function enables us to represent piecewise continuous functions conveniently. For example, consider the function

where we assume that and are defined on , even though they equal only on the indicated intervals. This assumption enables us to rewrite (eq:8.4.5) as To verify this, note that if then and (eq:8.4.6) becomes If then and (eq:8.4.6) becomes

We need the next theorem to show how (eq:8.4.6) can be used to find .

Let be defined on Suppose and exists for Then exists for , and

Proof
By definition, From this and the definition of , The first integral on the right equals zero. Introducing the new variable of integration in the second integral yields Changing the name of the variable of integration in the last integral from to yields

Find

Here and , so Since Theorem thmtype:8.4.1 implies that

Use Theorem thmtype:8.4.1 to find the Laplace transform of the function from Example example:8.4.1.

We first write in the form (eq:8.4.6) as Therefore

which is the result obtained in Example example:8.4.1.

Formula (eq:8.4.6) can be extended to more general piecewise continuous functions. For example, we can write as if , , and are all defined on .

Find the Laplace transform of

PIC

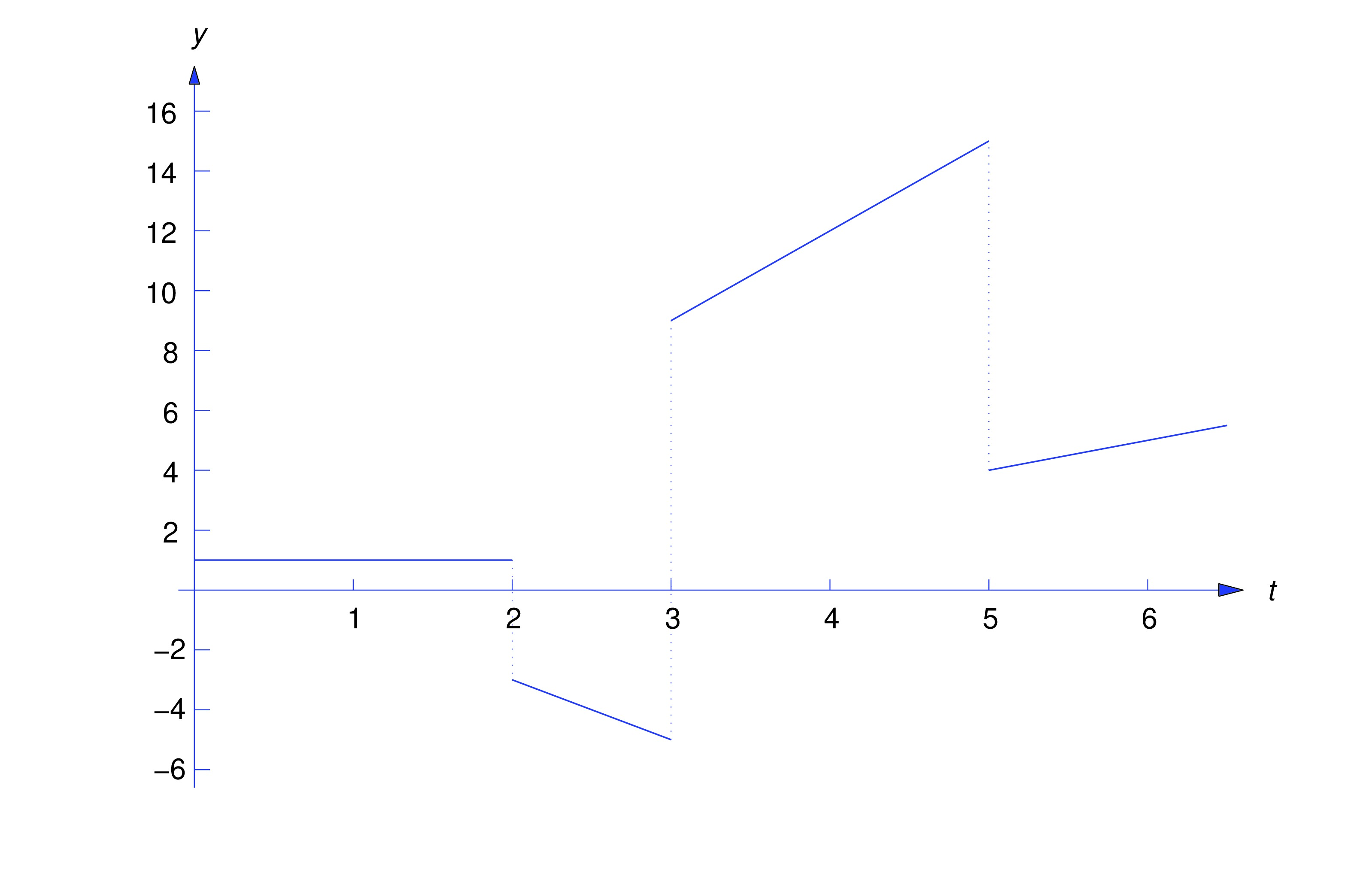
In terms of step functions,

or Now Theorem thmtype:8.4.1 implies that

The trigonometric identities

are useful in problems that involve shifting the arguments of trigonometric functions. We'll use these identities in the next example.

Find the Laplace transform of

PIC

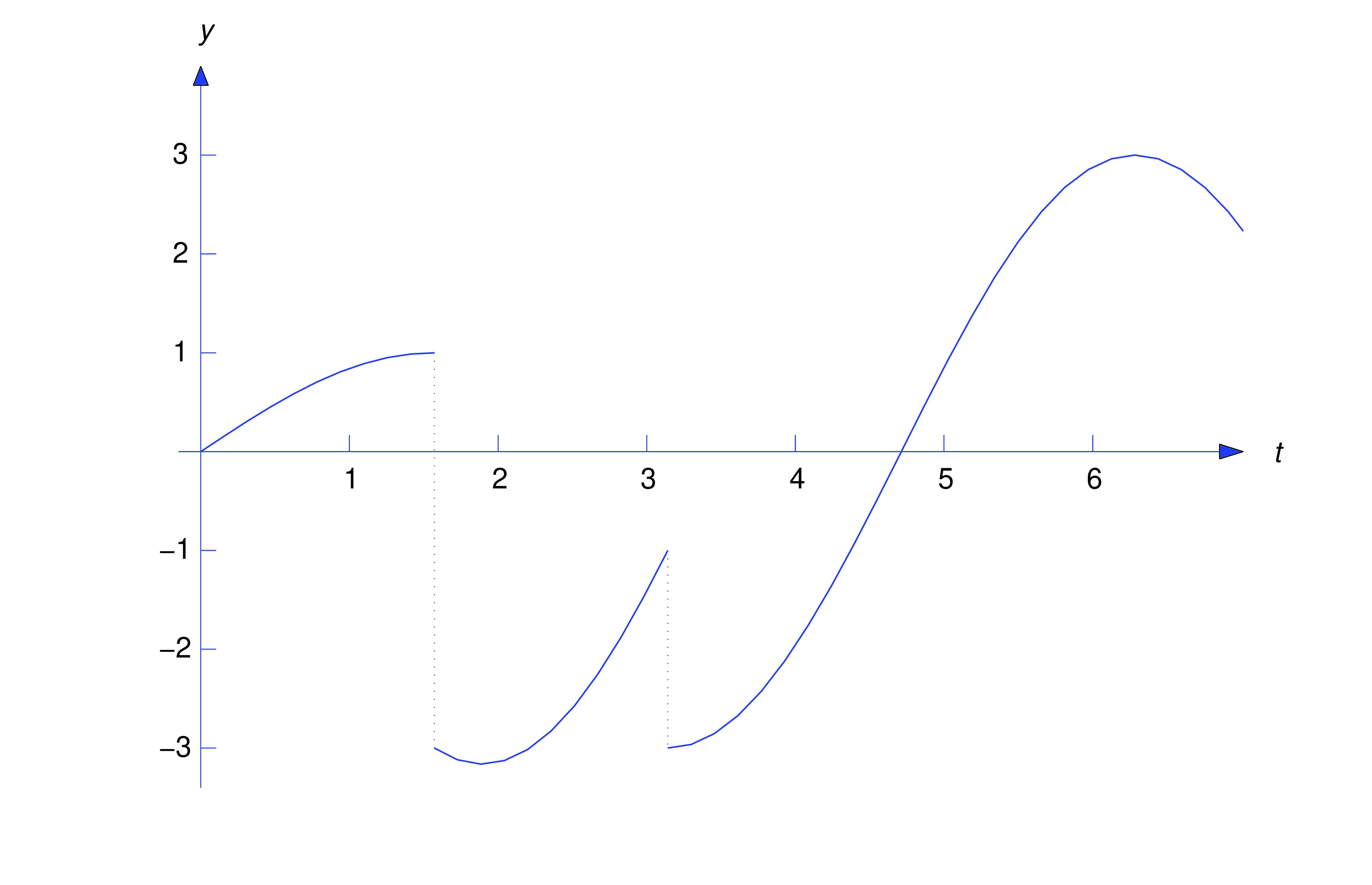
In terms of step functions, Now Theorem thmtype:8.4.1 implies that Since and we see from (eq:8.4.11) that

The Second Shifting Theorem

Replacing by in Theorem thmtype:8.4.1 yields the next theorem.

Second Shifting Theorem] If and exists for then exists for and or, equivalently,

Use (eq:8.4.12) to find

To apply (eq:8.4.12) we let and . Then and (eq:8.4.12) implies that

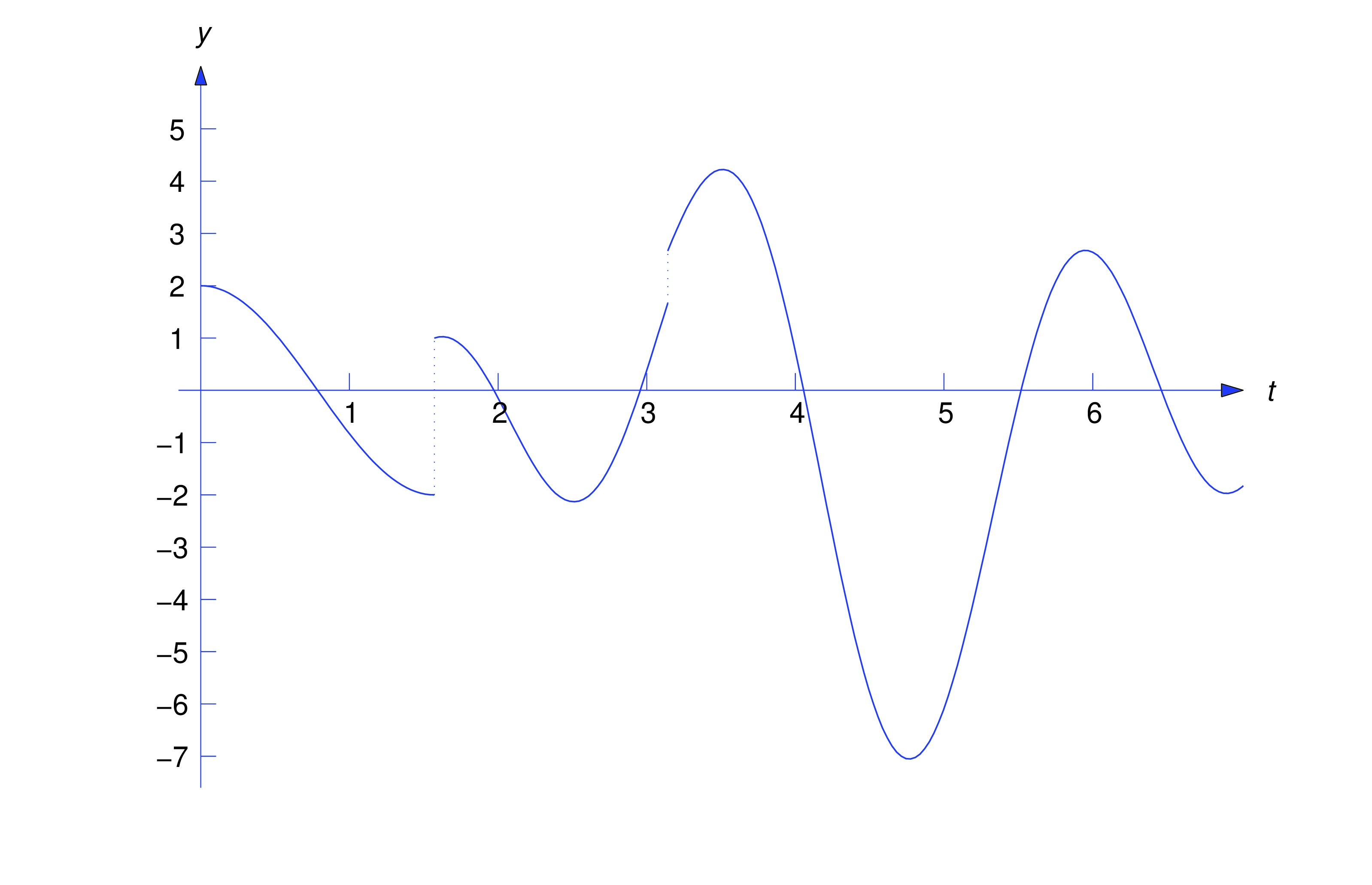
Find the inverse Laplace transform of and find distinct formulas for on appropriate intervals.

Let Then Hence, (eq:8.4.12) and the linearity of imply that

which can also be written as

Find the inverse transform of

Let and Then and Therefore (eq:8.4.12) and the linearity of imply that

Using the trigonometric identities (eq:8.4.8) and (eq:8.4.9), we can rewrite this as

PIC

Text Source

Trench, William F., "Elementary Differential Equations" (2013). Faculty Authored and Edited Books & CDs. 8. (CC-BY-NC-SA)

https://digitalcommons.trinity.edu/mono/8/